Line
vector pos0 = chv("pos0");
vector pos1 = chv("pos1");
int pt0 = addpoint( 0, pos0); //point1
int pt1 = addpoint( 0, pos1); //point2
int prim = addprim( 0, "polyline"); // primitive
//connect points to prim through vertex
addvertex( 0, prim, pt0);
addvertex( 0, prim, pt1);
Create a line for each point in primitive
int primitive = addprim(0, 'polyline');
int numberOfPoints = @numpt;
for (int n=0; n<numberOfPoints; n++){
addvertex(0, primitive, n);
}
y = 0 - Constant x
y = x - Linear
y = pow(2,x) - Exponential, these functions grow very rapidly. y = pow(M_E, x); y = exp(x);
y = pow(x,2) - Quadratic, same as: y = xx;
y = pow(x,3) - Cubic, same as: y = xx*x;
y = 1.0/x - Reciprocal, with x in the denominator this will produce asymptotes at the axis
y = log(x) - Logarithmic, rate of growth diminishes over time
y = sqrt(x) - Square Root, same as: y = pow(x,0.5);
Circle
int line = addprim(0,"polyline"); //draw
int a = ch("Angle");
float r = ch("Radian");
for(a=0; a<360; a++){
float x = cos(radians(a))*r;
float y = sin(radians(a))*r;
//draw
int point = addpoint(0,set(x,y,0));
addvertex(0,line,point);
}
int sample = chi("sample");
float radius = ch(""radius");
vector origin = chv("origin");
float two_pi = 3.1415*2;
float theta = 0;
float step_angle = two_pi/float(sample);
float x,z;
vector pos;
while( theta < two_pi){
x = origin.x + cos(theta) * radius;
z = origin.z + sin(theta) * radius;
pos = set(x, origin.y, z);
addpoint(0, pos);
theta += step_angle;
}
Logarytmic spiral

float e = 2.7182; // e
float r, x, y;
float a = ch("Angle");
float theta = radians(ch("Theta"));
float iterations = ch("Iterations");
int line = addprim(0,"polyline"); //draw
for(int i= 0; i < iterations; i++){
r = pow(e,a*(theta * i));
x = r * cos(theta * i);
y = r * sin(theta * i);
//draw
int point = addpoint(0,set(x,y,0));
addvertex(0,line,point);
}
- r = e^(a*theta)
Rhodonea Curve (sin @ polar)

float x,y;
float n = ch("n");
float d = ch("d");
float k = n/d;
float theta = radians(ch("Theta"));
int iterations = chi("Iterations");
int line = addprim(0,"polyline"); //draw
//Rhodonea Curve
for(int i = 0; i < iterations; i++){
x = cos(k*theta * i) * cos(theta * i);
y = cos(k*theta * i) * sin(theta * i);
//draw
int point = addpoint(0,set(x,y,0));
addvertex(0,line,point);
}
- k = n/d
- x = cos(k(theta))*cos(theta)
- y = cos(k(theta))*sin(theta)
Polar Limacon

float r;
float a = ch("a");
float b = ch("b");
float theta = radians(ch("Theta"));
int iterations = chi("Iterations");
int line = addprim(0,"polyline"); //draw
//Polar Limacon
for(int i = 0; i < iterations; i++){
float r = a + b * cos(theta * i);
float x = r * cos(theta * i);
float y = r * sin(theta * i);
//draw
int point = addpoint(0,set(x,y,0));
addvertex(0,line,point);
}
- r = a + b * cos(theta)
Lissajous Curve

vector pos = set(0,0,0);
float a = chf("a");
float b = chf("b");
float c = chf("c");
float maxiter = chf("MaxIterations");
int line = addprim(0, "polyline");
// Lissajous Curve
for(float angle = 0; angle < maxiter; angle += 0.01){
float x = cos(angle * a);
float y = sin(angle * b);
float z = cos(angle * c);
//draw
int point = addpoint(0, set(x,y,z));
addvertex(0, line, point);
}
Superformula 2D

int numsteps = chi("NumPoints");
float a = chf("a");
float b = chf("b");
float m = chf("m");
float n1 = chf("n1");
float n2 = chf("n2");
float n3 = chf("n3");
float rad = radians(chf("degrees"));
float step = (rad/numsteps);
float theta = 0.0f;
int line = addprim(0,"polyline");
// Superformula
for(int i=0; i<numsteps; i++) {
float c = pow(abs(cos((m*theta)/4) / a), n2);
float s = pow(abs(sin((m*theta)/4) / b), n3);
float r = pow((c + s), (1/n1)*-1);
// SOH CAH TOA (polar coords to x,z plane (cartesian))
float z = sin(theta) * r;
float x = cos(theta) * r;
//draw
int point = addpoint(0, set(x, 0, z));
addvertex(0,line,point);
theta += step; // increse theta by the step size before next loop iter
}
Superformula 3D
addpointattrib(0, "long", 0, "");
addpointattrib(0, "lat", 0, "");
int numsteps_long = chi("numPointsLong");
int numsteps_lat = chi("numPointsLat");
float a1 = chf("a1");
float b1 = chf("b1");
float m1 = chf("m1");
float n1 = chf("n1");
float n2 = chf("n2");
float n3 = chf("n3");
float a2 = chf("a2");
float b2 = chf("b2");
float m2 = chf("m2");
float n4 = chf("n4");
float n5 = chf("n5");
float n6 = chf("n6");
float step_long = ((2*$PI)/numsteps_long);
float step_lat = ($PI/numsteps_lat);
float long = -1*($PI);
float lat = -1*($PI/2);
for(int j=0; j<numsteps_lat; j++) {
for(int i=0; i<numsteps_long; i++) {
// Superformula A
float c1 = pow(abs(cos((m1*long)/4) / a1), n2);
float s1 = pow(abs(sin((m1*long)/4) / b1), n3);
float r1 = pow((c1 + s1), (1/n1)*-1);
// Superformula B
float c2 = pow(abs(cos((m2*lat)/4) / a2), n5);
float s2 = pow(abs(sin((m2*lat)/4) / b2), n6);
float r2 = pow((c2 + s2), (1/n4)*-1);
// 3D point plotting
float x = (r1 * cos(long)) * (r2 * cos(lat));
float y = (r1 * sin(long)) * (r2 * cos(lat));
float z = (r2 * sin(lat));
int pt = addpoint(0,set(x,y,z));
setpointattrib(0, "long", pt, i, "set");
setpointattrib(0, "lat", pt, j, "set");
// increse theta by the step size before next loop iter
long += step_long;
}
lat += step_lat;
}
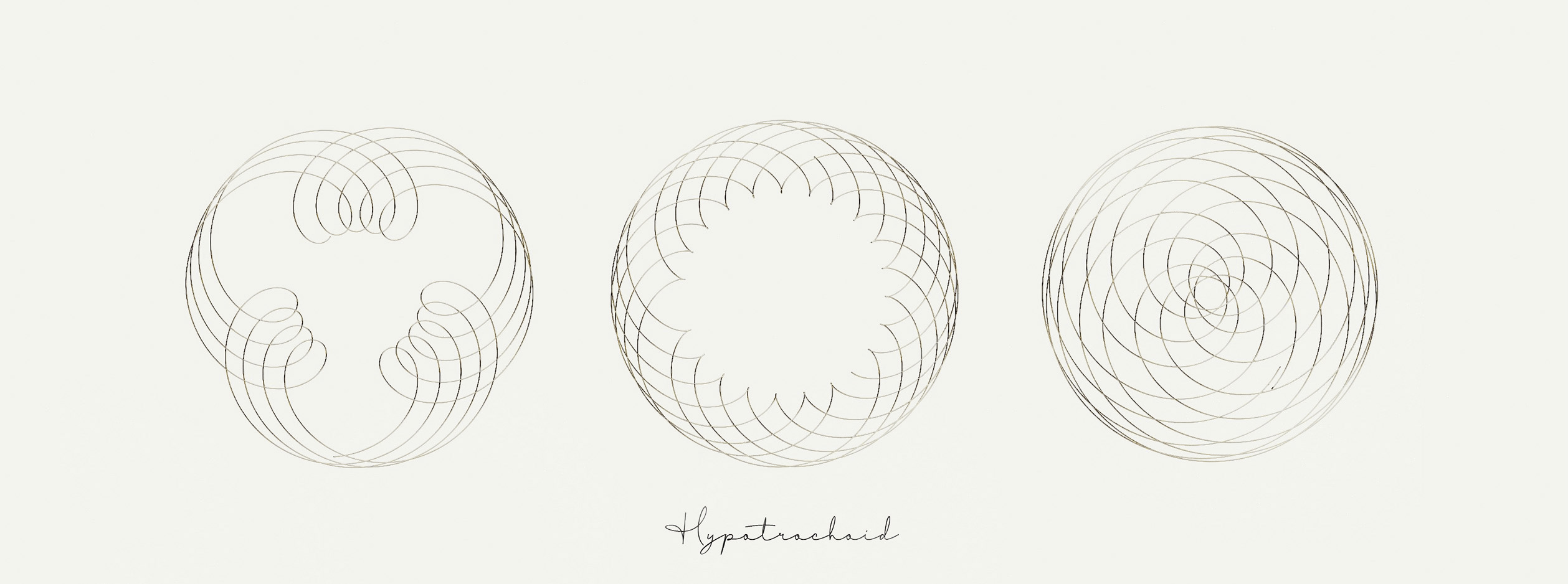
Hypotrochoid
float pi = 3.1415 // PI
float theta = ch("Theta") * pi * 2;
@theta2 = ch("Theta") * pi * 2;
float R = ch("R");
float r = ch("r");
float d = ch("d");
//Outer Circle
int R_circle = addprim(0,"polyline");
for(int i = 0; i < 400; i++){
float x, y;
x = R * cos(radians(1) * i);
y = R * sin(radians(1) * i);
int point = addpoint(0,set(x,y,0));
addvertex(0,R_circle,point);
}
//Rolling Circle
int r_circle = addprim(0,"polyline");
for(int i = 0; i < 400; i++){
float x, y;
x = r * cos(radians(1) * i) + (R - r) * cos(theta);
y = r * sin(radians(1) * i) + (R - r) * sin(theta);
int point = addpoint(0,set(x,y,0));
addvertex(0,r_circle,point);
}
//Center of rolling circle
float centerx, centery;
centerx = (R - r) * cos(theta);
centery = (R - r) * sin(theta);
vector center = set(centerx,centery);
int centerpoint = addpoint(0,center);
//Solve right triangle of center of rolling circle and origin
//Find hypotenuse
@hypotenuse = length(center);
vector origin = (0,0,0);
int originpoint = addpoint(0,v@origin);
int hypotenuseprim = addprim(0,"polyline");
addvertex(0,hypotenuseprim,originpoint);
addvertex(0,hypotenuseprim,centerpoint);
//Find adjacent
@adjacent = center.x;
int adjpoint = addpoint(0,set(@adjacent,0,0));
int adjacentprim = addprim(0,"polyline");
addvertex(0,adjacentprim,adjpoint);
addvertex(0,adjacentprim,originpoint);
//Find opposite with pythagorean theoream
float c = pow(@hypotenuse,2);
float a = pow(@adjacent,2);
@opposite = sqrt(c - a);
int oppositeprim = addprim(0,"polyline");
addvertex(0,oppositeprim,adjpoint);
addvertex(0,oppositeprim,centerpoint);
// Find all trig functions
float tan = @opposite / @adjacent;
float sin = @opposite / @hypotenuse;
float cos = @adjacent / @hypotenuse;
// Find all inverse trig functions
@arctan = atan(tan);
@arcsin = asin(sin);
@arccos = acos(cos);
//Solve
float rate = ch("Rate");
int hypotrochoidline = addprim(0,"polyline");
float hx = (R - r) * cos(theta) + d * cos((R-r/r)*theta*rate);
float hy = (R - r) * sin(theta) - d * sin((R-r/r)*theta*rate);
int hypotrochoidpoint = addpoint(0,set(hx,hy,0));
addvertex(0,hypotrochoidline,hypotrochoidpoint);
addvertex(0,hypotrochoidline,centerpoint);
//Make the trail
int hypotrochoidtrail = addprim(0,"polyline");
float resolution = ch("Resolution");
float iterations = ch("Iterations");
for(int i = 0; i < iterations; i++){
float x = (R - r) * cos(theta-(resolution*i)) + d * cos((R-r/r)*(theta-(resolution*i))*rate);
float y = (R - r) * sin(theta-(resolution*i)) - d * sin((R-r/r)*(theta-(resolution*i))*rate);
int point = addpoint(0,set(x,y,0));
}
- x = (R-r) * cos(alpha) + d * cos(R-r/r*alpha)
- y = (R-r) * sin(alpha) - d * sin(R-r/r*alpha)
- R is radius of outer circle
- r is radius of rolling circle
- d is displace amount (scalar multiply) applied to center of rolling circle to create trace point
Golden Points in circle

int num_pts = chi('NumPoints');
float radius = chf('Radius');
float radius_falloff = chf("RadiusFalloff");
float r;
float angle = 0;
float phi = (1 + sqrt(5)) * 0.5;
float golden_angle = 2 * $PI * (2 - phi);
vector origin = chv("Origin");
vector pos;
for(int i = 0; i < num_pts; ++i) {
r = radius * pow(float(i+1) / float(num_pts), radius_falloff);
angle = golden_angle * i;
pos = origin + set(cos(angle)*r, sin(angle)*r, 0);
addpoint(0, pos);
}
Arrange egzisting points in point wrangle log:
@P.x = chf("a") * pow(e, chf("b") * @ptnum * .001) * sin(@ptnum);
@P.z = chf("a") * pow(e, chf("b") * @ptnum * .001) * cos(@ptnum);
Spring on Curve
IN: spline > polyframe
[x] tangent
[x] bitangent
[x] make fram orthogonal
float rad=chf("radius");
vector dir=set(0,0,1)*rad;
matrix3 myMatrix=set(v@tangentu,v@tangentv,normalize(cross(v@tangentu,v@tangentv)));
3@myMatrix=myMatrix;
float rot=radians(chf("rotate"));
float sum=0;
for (int i=0; i<=@ptnum;i++)
{
float tempt=float(i)/(@numpt-1);
sum+=(chramp("rampRot",tempt)-0.5)*2/@numpt;
}
sum*=360*chf("scaleRamp");
f@integralRamp=sum;
rot+=radians(sum);
rotate(myMatrix,rot,v@tangentu);
dir=myMatrix*dir;
@P= @P+dir;
Strange Attractors
Svensson
int num = chi("num");
float a = chf("a");
float b = chf("b");
float c = chf("c");
float d = chf("d");
vector prevpos = set(0.1,0,0.1);
for(int i=0; i<num; i++){
float x = prevpos.x;
float z = prevpos.z;
float nx = d * sin(a * x) - sin(b * z);
float nz = c * cos(a * x) + cos(b * z);
vector npos = set(nx, 0, nz);
int npt = addpoint(0, npos);
prevpos = npos;
}